Ölçekten bağımsız şebekeler, gerçek şebekelerin en yaygın olanları arasında yer almaktadır. Genellikle, birçok sayıda bağlantıya sahip olan sınırlı sayıda noktanın yanısıra bunlara bağlı olan ve az sayıda bağlantıya sahip olan çok sayıda noktanın bulunduğu şebekelerle gerçek hayatta sıklıkla karşılaşırız. Bunun en iyi örneği, internetteki tüm sitelere bağlanmış olan Google şebekesi ile, Google’ın bağlantılı olduğu sitelerin daha az sayıdaki bağlantılardan oluşan şebekeleridir. Bir diğer örnek ise, yoğun merkezlerden (hub) ve ikincil hatlardan oluşan havayolu şebekeleridir.
Ölçekten bağımsız şebekeler, yapıları ve dinamikleri sistemin büyüklüğünden (N, sistemdeki nokta sayısı) bağımsız olduğu için karmaşık şebekeler arasında yer almaktadır. Bir başka deyişle, ölçek-bağımsız bir şebekenin tüm özellikleri şebekedeki nokta sayısından bağımsız olarak hep aynı olacaktır. Söz konusu şebekeleri diğerlerinden ayıran en önemli özellik ise, bu ağların derece dağılımının üssel bir nitelik arzetmesidir. Bu çerçevede, y birçok gerçek şebeke açısından 2 ila 3 arasında bir değerde olmak kaydıyla, bu tür şebekelerin derece dağılımı şu şekilde ifade edilebilir: P(k) ~ k¯γ
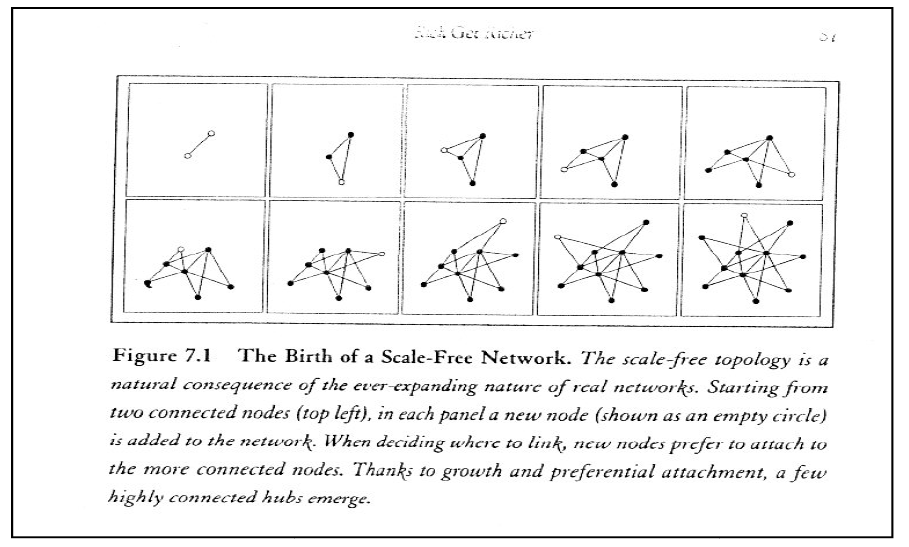
Bu alanda çalışma yapan Barabási and Albert1’in ortaya koydukları modele göre, ölçekten bağımsız bir şebekenin meydana gelmesinin ardındaki en önemli etkenler büyüme ve tercihli bağlantıdır. İlk etken, sistemin evrim sürecinde yeni noktalara bağlanılmasını açıklarken, ikinci etkene göre yeni noktalar diğerlerine oranla daha çok bağlantılara sahip olan noktalara bağlanma eğiliminde olacaktır. Bu mekanizma sonucunda, eş zamanlı olarak sisteme giren noktaların üst kuralını izledikleri ve ölçekten bağımsız şebekelerin karakteristik özelliklerinden olan büyük kümelenmelerin ortaya çıktığını görmekteyiz. Bağlantı sayısının bir noktadan diğerine eşit olarak değil de üssel olarak büyümesi süreci aynı zamanda “zenginlerin daha zengin hale gelmesi” şeklinde de ifade edilebilir.
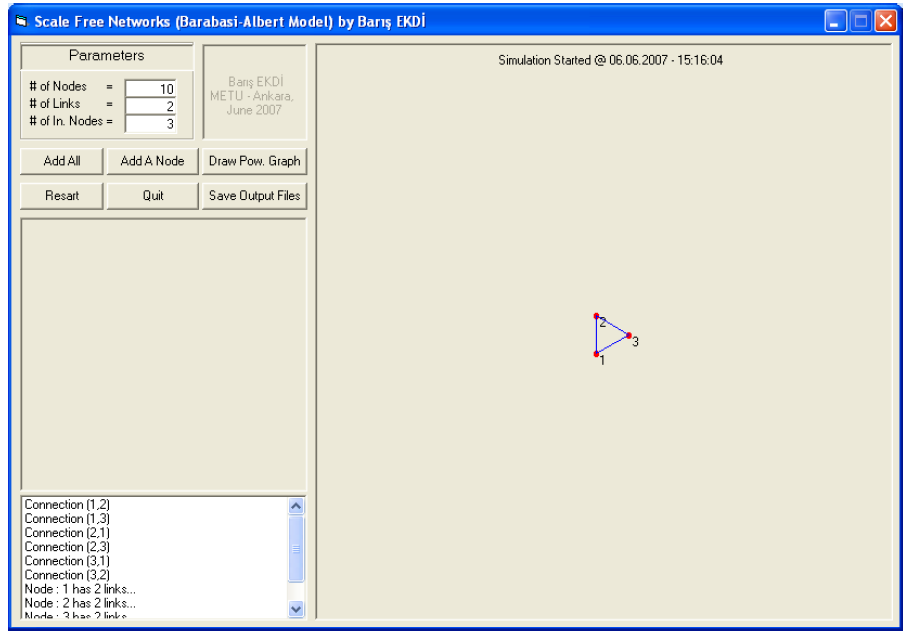
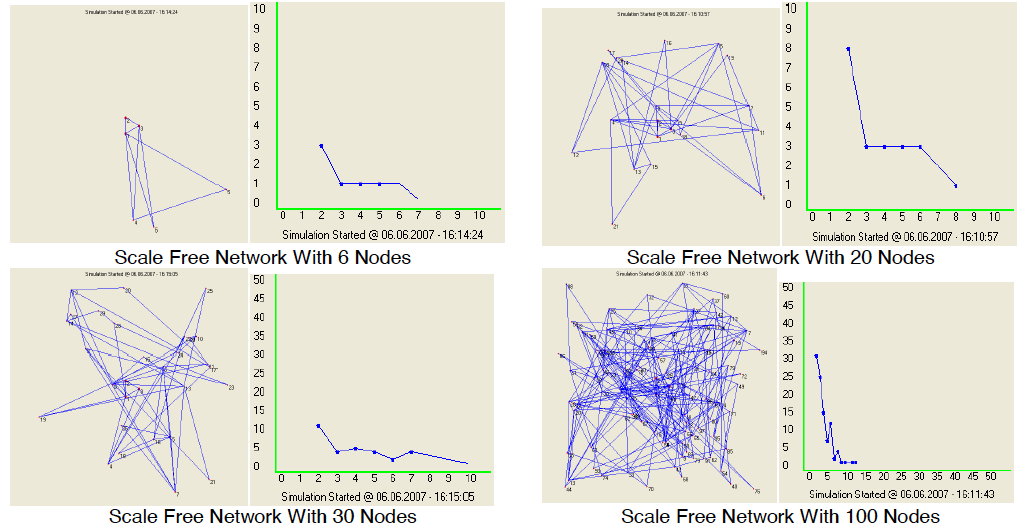
Simülasyon programına ilişkin İngilizce belgeyi okumak için yandaki simgenin üzerine tıklayınız:
1 Albert R. and Barabási A.-L., Statistical mechanics of complex networks, Rev. Mod. Phys. 74, 47–97 (2002). Barabàsi, Linked: The New Science of Networks, Perseus, Cambridge, MA, 2002.
